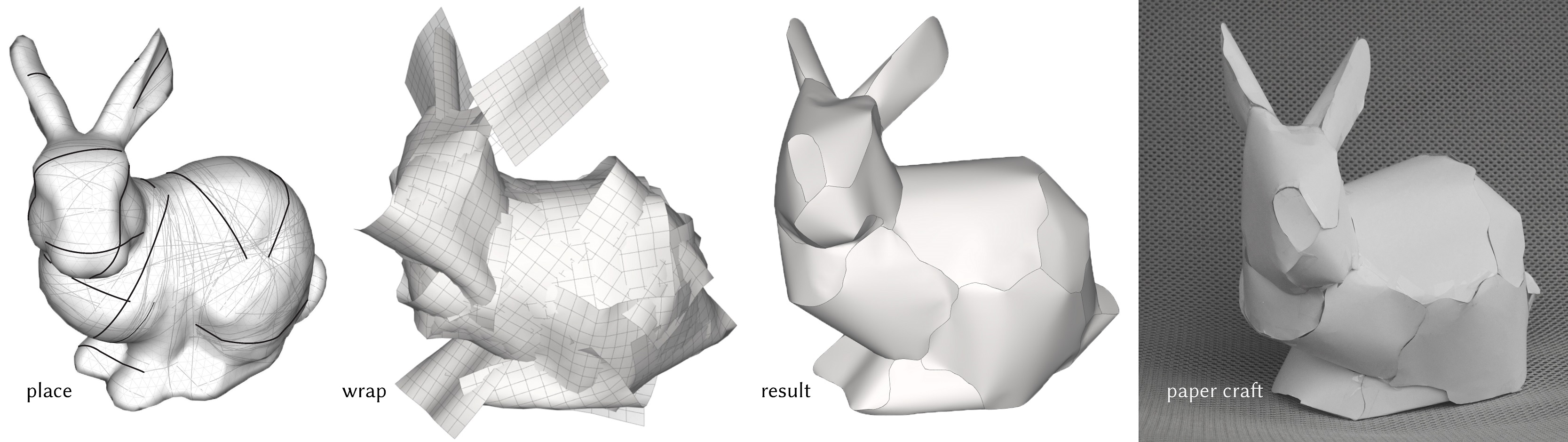
We present an automatic tool to approximate curved geometries with piecewise developable surfaces. At the center of our work is an algorithm that wraps a given 3D input surface with multiple developable patches, each modeled as a discrete orthogonal geodesic net. Our algorithm features a global optimization routine for effectively finding the placement of the developable patches. After wrapping the mesh, we use these patches and a non-linear projection step to generate a surface that approximates the original input, but is also amendable to simple and efficient fabrication techniques thanks to being piecewise developable. Our algorithm allows users to steer the tradeoff between approximation power and the number of developable patches used. We demonstrate the effectiveness of our approach on a range of 3D shapes. Compared to previous approaches, our results exhibit a smaller or comparable error with fewer patches to fabricate.
Publication
Alexandra Ion, Michael Rabinovich, Philipp Herholz, Olga Sorkine-Hornung. 2020. Shape Approximation by Developable Wrapping. ACM Transactions on Graphics 39, 6. (In Proceedings of SIGGRAPH ASIA 2020. Virtual conference, December 4 – 13, 2020). DOI: https://dl.acm.org/doi/10.1145/3414685.3417835